How To Graph Arithmetic Sequence

Definition and Basic Examples of Arithmetic Sequence

An arithmetics sequence is a listing of numbers with a definite design. If yous accept whatsoever number in the sequence and then subtract it by the previous one, and the consequence is e'er the aforementioned or abiding so it is an arithmetic sequence.

The constant difference in all pairs of consecutive or successive numbers in a sequence is called the common difference, denoted past the letter $d$ . We use the common difference to get from 1 term to another. How? Have the current term and add the mutual deviation to become to the next term, and so on. That is how the terms in the sequence are generated.

If the mutual divergence between consecutive terms is positive, we say that the sequence is increasing.
On the other hand, when the difference is negative we say that the sequence is decreasing.

Illustrative Examples of Increasing and Decreasing Arithmetic Sequences

Hither are 2 examples of arithmetic sequences. Find their common differences.

an example of increasing arithmetic sequence is 5, 9, 13, 17, ... in addition, an example of decreasing arithmetic sequence is 20, 17, 14, 11, ...

With this basic thought in mind, you can now solve bones arithmetic sequence problems.

Examples of How to Utilize the Concept of Arithmetics Sequence

Example one: Find the next term in the sequence below.

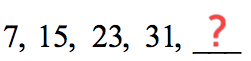
First, find the common difference of each pair of consecutive numbers.

$15-7 = eight$

$23-15 = viii$

$31-23 = 8$

Since the mutual deviation is $8$ or written as $d=8$ , we can find the side by side term after $31$ by calculation $8$ to information technology. Therefore, nosotros take $31 + 8 = 39$ .

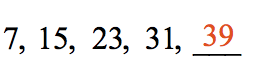
Example 2: Discover the side by side term in the sequence below.

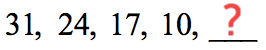
Discover that the sequence is decreasing. We expect to have a mutual departure that is negative in value.

$24-31 = -7$

$17-24 = -7$

$10-17 = -7$

To go to the next term, we volition add this common difference of $d=-seven$ to the last term in the sequence. Therefore, $10 + \left( { - vii} \right) = iii$ .

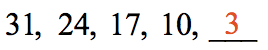
Example 3: Find the side by side three terms in the sequence below.

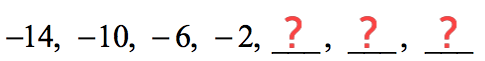
Be careful here. Don't assume that if the terms in the sequence are all negative numbers, it is a decreasing sequence. Remember, it is decreasing whenever the common difference is negative. So allow's notice the common difference by taking each term and subtracting information technology by the term that comes before it.

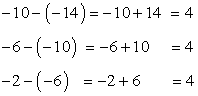
negative 10 minus negative 14 equals 4 negative 6 minus negative 10 equals 4 negative 2 minus negative 6 equals 4

The common divergence here is positive four $\left( { + \,4} \right)$ which makes this an increasing arithmetics sequence. Nosotros can obtain the next three terms by adding the concluding term by this common difference. Whatsoever is the outcome, add again by $4$ , and do it one more time.

Hither'due south the calculation:

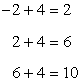
The next 3 terms in the sequence are shown in red.

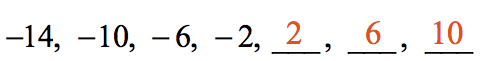
Example 4: Find the seventh term (vii^th) in the sequence beneath.

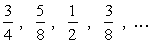
Sometimes you may encounter a problem in an arithmetic sequence that involves fractions. So be ready to use your previous knowledge on how to add or subtract fractions.

Besides, e'er make sure that you understand what the question is asking so that you tin can accept the correct strategy to approach the trouble.

In this case, nosotros are asked to discover the seventh term, not merely the next term. Information technology is a skilful do to write all the terms in the sequence and label them, if possible.

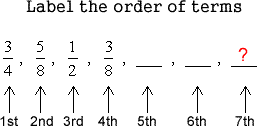
find the fifth, sixth, and seventh terms of the sequence 3/4, 5/8, 1/2, 3/8, and so

At present we take a clear understanding of how to work this out. Find the common difference, and use this to observe the seventh term.

Finding the mutual difference,

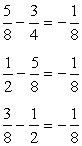
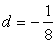
the common difference is negative one-eight

So we observe the seventh term by calculation the mutual departure starting with the quaternary term, and so on. Hither'due south the complete calculation.

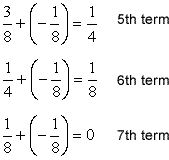
the fifth term is 1/4 the sixth term is 1/8 the seventh term is 0

Therefore, the seventh term of the sequence is zero (0). We tin write the terminal answer as,

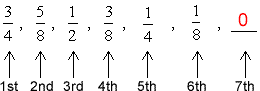
Instance 5: Find the $\color{red}{35^{thursday}}$ term in the arithmetic sequence $3$ , $ix$ , $fifteen$ , $21$ , …

Yous tin can solve this problem by listing the successive terms using the common divergence. This method is tedious considering you will have to continue calculation the common difference (which is $6$ ) xxx-v times starting with the last term in the sequence.

You lot don't have to do this considering information technology is cumbersome. And not only that, it is easy to commit a careless error during the repetitive add-on procedure.

If yous make up one's mind to find the $\color{carmine}{35^{th}}$ term of the sequence using this "successive improver" method, your solution will wait similar below. The "dot dot dot" means that there are calculations at that place but not shown equally information technology can easily occupy the unabridged page.

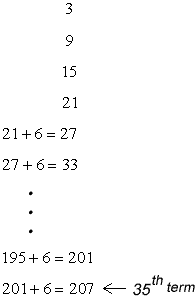
Yous might besides be interested in:

Arithmetic Sequence Formula

Arithmetics Series Formula

More Practice Problems with the Arithmetic Sequence Formula